
SQGY06 色情公寓EP6-尤莉的!

もとめてンス

91MS-011語文老師

街头素人搭讪2 洛雪

1人分のザー

マブダチとレズれ!inみなとまち 今井夏帆 松本一香

【精品视频】娇嫩小白虎,清纯与淫荡的极度反差

国产AV 杏吧 背着男友偷情富二代 腕儿!

兔子先生TZ-038東京愛欲故事EP4

TMW08巨乳女友聖誕驚喜

我和老师朋友的妈妈2

¥$マニー¥$の虎 志願者たちよ貴女の未来に投資します! 事業計画のビジョンを話していたらアソ的!

るらしいになって
![[Pashmina]纯情少女エトセトラ~ネット▼ラブ~](https://lsbzytp.com:3519/upload/vod/20231010-1/4b3896bfa858a03f50aa590e561bbb30.jpg)
[Pashmina]纯情少女エトセトラ~ネット▼ラブ~

偷拆包裹的惩罚1

麻豆传媒-毒舌巨乳女邻居为钱成低贱肉便器-白若冰

XK805 無間道2-秋霞的!

オイルマッサージで発情メス堕ち 禁断のアヘアヘ本番記録的!

股人タクシー 获物2 姉妹狩り?玲名と瀬名

你的小鹿鹿

女优初面试-真枪实弹直接操.

XK8051 無間道2-秋霞1
![【有码中字】[メリー?ジェーン]おやすみせっくす 第4话あふれ出る想いが止まらない朝.chs](https://lsbzytp.com:3519/upload/vod/20231010-1/81c50b7e62d08ace1ac6b21931dfcca7.jpg)
【有码中字】[メリー?ジェーン]おやすみせっくす 第4话あふれ出る想いが止まらない朝.chs

21时の女1!

摄影师外拍直接骑上性感模特1

【水果派】《黑暗圣经》清纯少女遭爆菊,淫荡属性被激活!1

想確認愛意的妻子和絕倫後輩 二人獨處的三小時... 不拔出的追擊中出17發 黑川堇

黄金搭档@18p2p→92新女性宝鉴←.

学园的守猎者1

眼睛屌丝男潜规则两个漂亮女助理 双飞小骚逼轮着操

Sakurato.sub04

妻子出轨我最好的朋友的!

处女们,任何污淫

91CM-170 穿越到王者榮耀的世界-謝語彤1

禁断·義父と嫁 ~息子は知っている私たちの関係~

少女的踩躏调教!滚烫蜡油滴满丰乳美腿!竹棍鞭打屁股尖叫连连1

鸭哥寻欢深夜网约极品高端外围

情侣自拍

第一次对镜头大潮吹-辛尤里1的!

性感短裙美女和网友吃饭后到会所包厢等按摩技师时按耐不出掀开短裙啪啪,搞完后又到酒店继续操,床都干歪了!

纯天然大胸很少见,大屌爆操小骚逼,睡卧莲花1的!

KTV里的性爱歌摇的!

无敌肥臀嫩穴

【水果派】被男友卖掉后被轮奸!1

国产精品偷拍-长腿高冷嫩模 线下约炮1的!

JDSY003 縱欲小姑強上快遞員到高潮1

约到的肉弹丰满女孩直接去旅馆整天无套中出

STARS-657 『世界で1番エロいキスしてみない?』理性を忘れて舐めまくる感じる唇、終わらない接吻。 小倉由菜

TMY0026周末宅家插妹妹的!

麻豆传媒-JK主播的迷奸餐强力春药拘束调教-张小九

麻豆传媒-深夜舒压会所-夏晴子

ストリンジェンド&アッチェレランド ULTIMATUM~SERA~#1

终电后, カプセルホテルで, 上司に微热伝わる夜

横扫全国外围圈

愛人(梨穂)と温泉中出し不倫妻が出張で不在の二日間

3D 最终幻想萨那鲁刚多那一夜

爆操内射清纯乖乖女,第一段!

バカな妹を利口にするのは俺の××だけな件についてコスプレ爛漫!!御津井芭華一番好きなのは、お兄ちゃん編

媳婦的誘惑 香椎佳穗

我不是因为你而长大的

捆绑调教饥渴母狗肉棒满足1

驚愕の放課後SEXレポートを公開します!とある調査によると近年ではZ世代の若者半数以上が男女共的!

JD038 輪回酒店1

【小鸟酱】白丝足交 诱惑动人1
![[milky] 艶母 taboo-1 「満たされぬ人妻」](https://lsbzytp.com:3519/upload/vod/20230910-1/8a0eaf02531b8bd42cce2d5cb17261cc.jpg)
[milky] 艶母 taboo-1 「満たされぬ人妻」

刚结婚不久小少妇出道,沙发后入口爆。

小肥猫咪

千人斩探花 2020.08-09 【AI高清2K修复】千人斩星选深夜场纹身妹子玩3P,倒立口交一前一后轮着操非常刺激

草莓巧克力香氛1

大尺度私拍时被摄影师趁机揩油用道具玩弄嫩穴

麻豆传媒-下班后的搔痒难耐-夏禹熙

【水果派】和S1七姐妹同居的后宫性生活1
![[milky] 愛のカタチ scene1 ~エッチな女のコは嫌い ですか?~](https://lsbzytp.com:3519/upload/vod/20230910-1/da597245a394c93cd0a43329fe70a214.jpg)
[milky] 愛のカタチ scene1 ~エッチな女のコは嫌い ですか?~

HEYDOUGA4030-2249 佐々木優奈-土下座懇願 M痴女

小美女想当演员,只好先用肉体取悦没什么名的导演

中文对白-黑丝淫语老师的诱惑1

91CM-156 反常的妻子-徐慧慧

上门卖延迟避孕套的学生,美女成了试验品,被操到腿抽筋

被欲女女友榨干

麻豆传媒-妹妹房间的冷气坏掉-徐蕾

无意识屁股受不了失控后背活塞运动

XK807 少妇白洁5爱是一道光的!

巨乳千金在学园 第一话

TMY0006 偷窺媽媽自慰

XK8125 新娘媽媽

在户外被男生轮奸

91CM-204 迷奸清純女同學-白雪

淫行教師4 feat.エロ議員センセイ 静歌&初音~ガラス越

美女老板变身性公司奴隶的!

「悲惨娱乐圈」为上位被潜规则无套玩弄的!

恋人的调情记录的!

xsj048-被潜规则的实习生1

SWAG『bridget』

2022 KIN8 AWARD 5位-1位発表 BEST MOVIE OF THE YEAR #
![プライベートエモーション [第二章 梦の终わりに…]!](https://lsbzytp.com:3519/upload/vod/20231010-1/87c3626eb74ef8e0553dfa5002c40a0e.jpg)
プライベートエモーション [第二章 梦の终わりに…]!

网约极品外围女神清纯脸庞,大长腿翘臀美乳

同性恋的性爱

现役女高中生下海家庭教师指导性爱首次破处

清纯妹子被操的呻吟不断1

大街上挑素人约炮

有个小骚货女朋友,真的幸福啊
![[HENTAI] HOT-HENTAI-BONDAGE-MILF REALSEX](https://lsbzytp.com:3519/upload/vod/20231010-1/c6505f19585507451f3f70a9fc9c039e.jpg)
[HENTAI] HOT-HENTAI-BONDAGE-MILF REALSEX

小性奴张开双腿求主人填满1

自宅警备员 3

处女开苞,学生妹6000快卖掉初夜

XK8048 少婦白潔3-童汐的!

肉感秘书室,秘书的射精业务报告的!

超诱惑妝妝xBetty纯洁的修女姿色太诱人

航空空姐与公司高层性爱视频

美少女出租的!

爱丝袜的Vivian姐_中国风内衣酒店内后入最后口爆的!

甜美小姐姐水晶屌插逼1

约炮行动与同事的秘密性爱

夜勤病栋ヒロインシリーズ 八神优

NSFS-057 被捲進某個時間的妻子 妻子被男人們當成洩慾目標 淺宮千夏 聖菜亞里沙

Tentacle and Witches 第1话 俺、触手になりました

3D 魅魔双姐妹1

一秒都不想錯過 在妻子老家被義姐走光誘惑 危險中出性交 小松杏

JDMY038 密友第三十八集1

制服少女さくらたんと学校でこっそり声我慢SEXしたい人いる??的!

大叔 陪我玩吧 一日限定的壞孩子 志木舞奈

柚子猫Cosplay第一次被口爆,好吃吗?

TM067好色鄰居搞媽咪的!

【Yuri】中式旗袍美乳做爱被中出的!

长发美女酒店有点害羞不让操小伙软磨硬泡半天插进去干了她

3000约外围,躺在胯下狂插!

176CM性感翘臀高跟大长腿美女和客人酒店啪啪,屁股超性感!!
![人妻、蜜と肉 第三巻[月野定规]](https://lsbzytp.com:3519/upload/vod/20231010-1/77b5761abdb73b3c0415e46d8daf38dd.jpg)
人妻、蜜と肉 第三巻[月野定规]

まさかの初AV出演! 初生ハメ、初中出し! 初めてカメラの前でイッちゃいました~ 8人的

SweetHome~Hなお姉さんは好きですか?~「三甘」

麻豆传媒-女记者实况骚播-顾桃桃

强上美女纹身师一边操一边叫宝贝

尝试野外天台调教

害羞,迷戀,高潮停不了。 約會中被指令不自由還有試著做痴女!二天一夜一狂抽插的溫泉約會 東雲美玲

寝取られ堕ちた女たち- 女教师 黒瀬胜子编

性感火辣学姐被隐形男后入!强奸!

JD058鄰家母女之隔壁張叔給我破處

【精品推荐】渣男干完不给钱直接把美女逗哭了

3D 魅魔双姐妹2

JDSY018爆操住家小保姆1

TM0143 艳母5-肉体与灵魂的双重堕落

MIRD-202 一夫多妻制2 大嫌いな中年オヤジと強●ハーレム中出し! 今井夏帆 蓮實克蕾雅 八乃翼

穿着开裆裤拿震动棒自慰的小美女

JUL-098 車中泊NTR ―社員旅行の帰り道、ドライブレコーダーに記録された汗だく中出し映像― 栗栖みなみ

一打开门就立刻做爱

性感黑丝OL下班寂寞在家自慰1

3D 被我征服的巨乳女佣

【柚子猫】《原神》复刻.五星女神刻晴对旅行者的性处理

9 男が夢見る超絶カワイイ美少女との究極イチャイチャラブ5シチュエーション ‘22梅雨 西元明沙

黑大鸡巴电召年轻少妇被狂干

【SA国际传媒】 SAT-0076《超近公务员》上班执行秘密公务(上)

【麻豆传媒】MDWP-0021 淫行肉便所,野外露出的视奸快感-唐霏

麻豆传媒-请用你的肉棒训练我

5 下校少女連れ去り監禁ガンギマリ肉便器 ターゲット潮吹き天使的

大三的性感美女课余时间兼职被摄影师潜规则,床上干完凳子上干

E奶蝶大戰黑人+兩支大屌男優的!

桜都字幕组ばにぃうぉ~か~OVA屈辱#2

酒店约操90后小兼职少妇

ふくびき!トライアングル ~美晴アフター~ ~エロ萌えびっち変态连呼姉妹のおっきぃ骂り◆~ 二

TM0162性愛筆記1
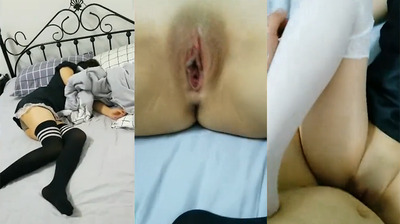
药物眠姦迷奸超美学生内射奸淫粉嫩小穴无毛白虎

格格骚到骨子里喜欢熟女必看

あらいめんとゆーゆー THE ANIMATION Ghost

TM029巨乳少婦成了我的室友的!

【网曝门事件】香港曾经地产经理马纪筠BelleMa性爱访谈+2017因FOXY软件性爱视频流出口交篇

JDYP006 嗑藥男爆操約啪妹-夏夏

【91制片厂】91CM-234 肉感精油SPA,痉挛停不下来 性感开发精油按摩-酒井爱

太子探花 2020.08-09 【AI高清2K修复】2020.9.15 太子探花极品高颜值鸭舌帽妹子,翘屁股掰穴69口交大力抽插猛操

剑奴.1993

上班族OL的吊带黑丝深喉激烈性爱1

姨母的誘惑31

麻豆传媒-清纯女店员-孟若雨

TM0141被欺凌的高中校花21

超有感觉的美少女伴着音乐裸舞自慰!插的自己痉挛抽搐尖叫连连1的!

91CM067 網貸1

一个长腿的女士欺负一个受虐狂的男人

超性感美女高清视频,大长腿,白屁股

极度淫荡骚女3P名场面!两根大屌左右一起舔!操穴插嘴齐开,喜欢射在嘴里,吸吮JB太骚了

誒?要在這裡中出?人氣AV女優被炮友要求像AV一樣的中出SEX 川上奈奈美

最骚瑶妹化身翘臀精灵保护你的肉棒拯救你的灵魂1

三亚淫乱夜?前后夹击极品反差婊1

NNPJ-581 「脱いでくれたら入会するよ。」 マルチ勧誘の女ホテルに連れ込んで生ハメカウンター喰らわせてヤッ

爱圣天使ラブメアリー~悪性受胎~

28 170cm顶级美腿女神第一骚女暴力自慰,各种道具万物皆可插,大茄子撑爆小穴,高跟鞋爆插菊花,棒球棍站立骑坐
![[ピンクパイナップル]PRETTY×CATIONTHEANIMATION#1初恋、それぞれの距离](https://lsbzytp.com:3519/upload/vod/20231010-1/7155738cc22bbe5bc2fd237249f66b2e.jpg)
[ピンクパイナップル]PRETTY×CATIONTHEANIMATION#1初恋、それぞれの距离

麻豆传媒-珠算老师的独门技巧-白靖寒

【水果派】办公室媚药打炮恩仇录1

小伙网约大长腿极品美女,跪地舔弄奶头,性感黑丝舔屌口交,张开双腿一顿草

高颜值苗条妹子和炮友浴室后入猛操非常诱人_很是诱惑

麻豆传媒-突袭女优家EP9-欲火难耐逆推摄影师-袁子仪

【JVID】全空巨乳淫尻想要和你来场鱼水之欢的!

苗条的正妹酒店硬搞

斗破苍穹纳兰嫣然

骚少妇户外野地跳蛋塞逼自慰 回到车上掰开近距离特写毛毛挺浓密

TM0126 黑暗幼女-安妮

91CM-149 家教老師-謝語彤1
![[メリー?ジェーン]女子高生の腰つき ビーチバレー部編 Round 2](https://lsbzytp.com:3519/upload/vod/20231010-1/4b890936272deefd5d0c5b2b66d2a47f.jpg)
[メリー?ジェーン]女子高生の腰つき ビーチバレー部編 Round 2

大神直播小骚妇主播户外约了个猛男带回家啪啪下面毛多性欲强!